实现一个数学表达式的解析执行器

最近我们在一个项目中实现了一个小型解释器。这个解释器实现了一种简洁的表达式语言，支持常见的数学函数、向量运算和类 jsonpath 语法。整个实现由 Lexer、Parser 和 Executor 组合而成，共同实现了一个符合 LL(1) 文法的表达式语言。

在这个项目中，我们希望能够实现一个支持向量运算、常见数学函数的数学表达式计算器。它能够接受任意的用户输入的数学表达式，并计算得到结果：

c = sin([1, 2, 3] * 2) - 0.1
# expected c = [ 0.80929743, -0.8568025 , -0.3794155 ]

此外，我们还希望能够支持一种类 jsonpath 语法，以便快速获取 context 的数据流。我们把这个表达式语法称为 JsonRoute，避免和 jsonpath 混淆：

hp_percentages = [$].heros[*].hp / [$].heros[*].max_hp * 100
# $ 是一个全局 iterator
# * 表示取列表所有值

这里的挑战在于：

对用户输入的表达式进行语法检查，不合法的需要拒绝；
支持各种常见的数学运算符，并保持它们参见的运算符优先级；
支持参见的数学函数；
支持向量运算，如常见的 broadcast、dot operator

由于产品的需求，这个计算过程需要实时跑在前端上，所以我们无法直接使用如 numpy 等常用的 Python 库。

1. 整体流程

定义一个 LL(1) 文法，描述表达式语言的完整语法，它将指导我们的后续实现
实现一个 Lexer，按照语法的基础元素进行分词，同时实现基础的词法分析
实现一个 Parser，根据语法和 token 序列，构建一颗完整的语法树，同时实现语法分析
实现一个 Executor，直接执行得到的这颗语法树，输出最终结果

LL(1) 文法足够简单，它良好的上下文无关、无左递归、无二义性的特性，使得我们的实现变得非常简单。

2. 文法

这里的文法非常简单，主要注意符号的优先级即可：

// 与或非
expr -> expr && term | expr || term | !term | term
// 条件判断
term -> term > factor | term < factor | term != factor | term <= factor | term >= factor | term == factor | factor
// 加减法
factor -> factor + group | factor - group | group
// 乘除法
group -> group * value | group / value | group % value | value
// 正负号
value -> +subexpr | -subexpr | subexpr
// 括号、函数、jsonRoute 表达式、数字常量
subexpr -> (expr) | funcCall | JsonRouteExpr | num
// 函数调用，支持嵌套的函数、表达式
funcCall -> keyword(args) | args -> expr | expr, args

如果要实现三元表达式，我们还可以在 subepxr 处加上它的定义：

subexpr -> (expr) | funcCall | JsonRouteExpr | num | expr ? subexpr : subexpr

接着，我们需要消除掉所有左递归的定义。具体这里不多赘述，ChatGPT 就能求解得很好。

3. 实现 Lexer

Lexer 需要把输入的表达式文本做分词（tokenizer），同时检查基础语法，如括号是否匹配，二元表达式是否有左右两侧的子表达式（如除法，必然有左右两侧的子表达式）。

这里给出一个 Python 伪代码，实现非常简单：

while curPos < end:
	skipWhitespace()
	token = expression[curPos : curPos+2]
	if dualOperands.includes(token):	# 双字节字符：如 && || <= >=
		consumeDualOperand(token)
        curPos += 2
		continue
    ... # 同理实现单字节字符如：< > + - * /
    token = re.split(r'\s', expression[curPos:], maxsplit=1)[0]
    if re.match(r'^[0-9]*.{0,1}[0-9]+$', token):	# 数字，可能带小数点
		consumeNumber(token)
        curPos += len(token)
       	continue
    if token := re.match(r'^[a-z_][a-z_0-9]*\(.*\)', expression[curPos:], re.IGNORECASE):	# 函数，如 func(a,b,c)，这里只处理函数名，参数是表达式
        funcName = parseFuncName(token)
		consumeFuncName(funcName)
        curPos += len(funcName)
        continue
	# 继续实现其他符号的分词和解析
    ...
    # 用 stack 来检查括号是否匹配
    stack = []
    for t in tokens:
        stack.rpush(t) if t in LPAREN else None
        if t in RPAREN:
            lhs = stack.rpop()
            if not match(lhs, t):
                raise SyntaxError("bracket not matched")

4. 实现 Parser

Parser 根据 Lexer 生成得到的 token 序列，依据前面设计的 LL(1) 文法，来驱动解析过程，构建出一颗语法树。如消除左递归后的加减法过程的实现：

# factor  -> group factorTail
# factorTail -> + group factorTail | - group factorTail | e   e 为终结符

def parseFactor(self) -> AstExpression:
	lhs = self.parseGroup()		# group 表达式
	return self.parseFactorTail(lhs)	# factorTail 表达式

def parseFactorTail(self, lhs: AstExpression) -> AstExpression:
	if self.lexer.eof():	# 终结符 e
		return lhs
	token = self.lexer.peek()
	if (token.type == TokenType.OPERAND) and (token.value == '+' or token.value == '-'):
		self.lexer.consume()
		rhs = self.parseGroup()		# group 表达式
        return self.parseFactorTail(BinaryAstNode(self.expression, token, lhs, rhs))
    else:
		return lhs

可以发现，根据无左递归的 LL(1) 文法来写代码是非常简单的，就是把它翻译为一个个函数调用即可。最终我们将得到类似这样的一颗语法树：

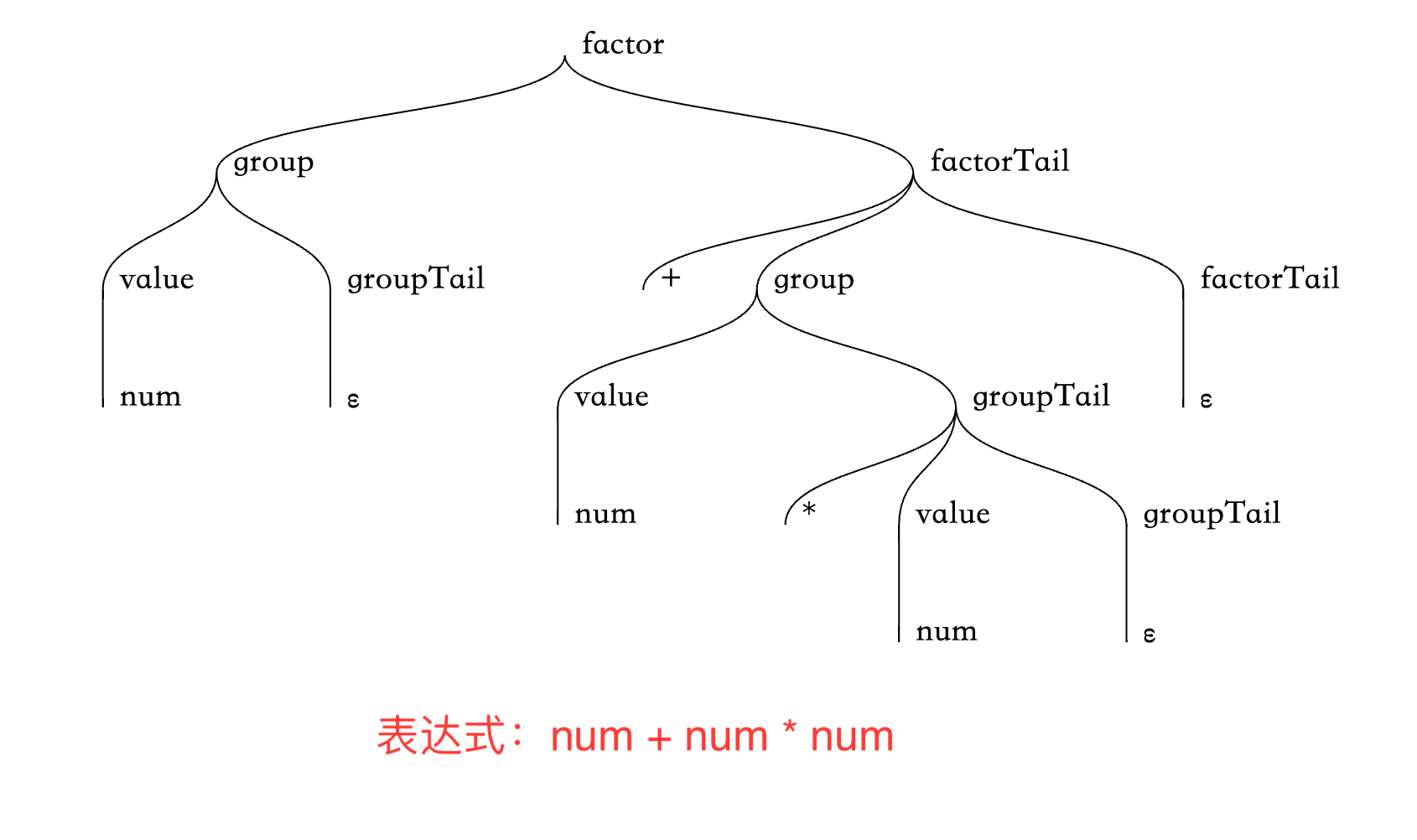
或者复杂一些，加上括号优先级的：

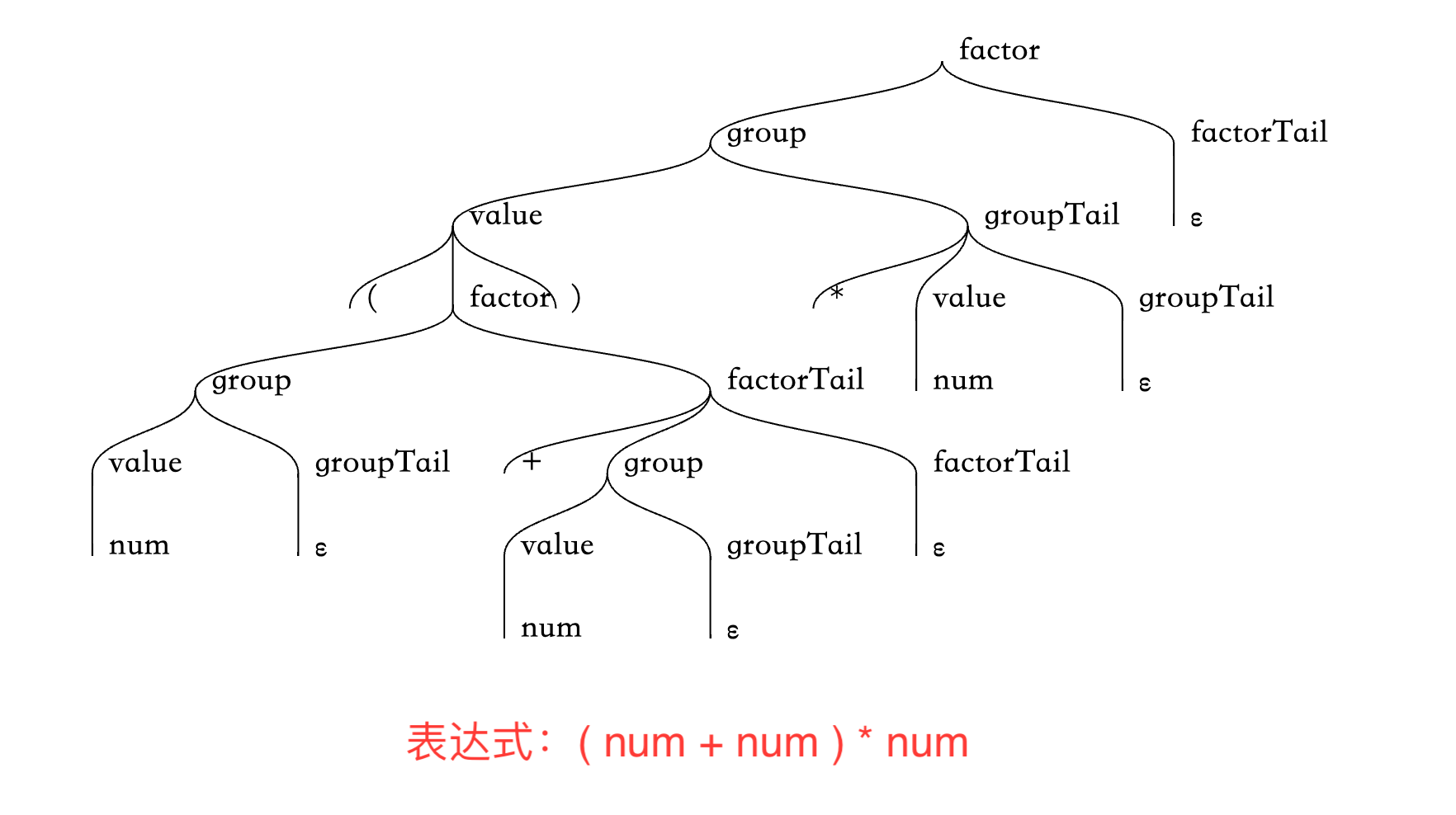
5. 实现 Executor

当我们构造出语法树后，Executor 的实现就变得很简单了。我们对这棵树按照先序遍历的方式（左侧节点优先），逐一执行各个节点即可。

比如这里给出一个二元运算符的节点，执行一个二元运算符，如 a + b，我们需要知道：

二元运算符的左侧表达式结果，即这里的 a，它可以是一个非常复杂的表达式的计算结果，如（1+2*3-4)，但在当前加法这个二元运算符的上下文里，我们并不关心这个表达式的具体内容，我们只需要知道，它目前的值是 a 即可
二元运算符的右侧表达式结果，同样的我们并不关心它的具体内容，它目前的值是 b
二元运算符本身，如这里的加法。减法、乘除法等照猫画虎即可

当我们得知了这三项内容后，求解就是把它们相加即可：

class BinaryAstNode(AstExpression):
	operand: Token
	lhs, rhs: AstExpression
    
    def eval(self, context):	# context 用来传递一些全局变量信息，供给 JsonRoute 等表达式使用
        lhs_value = lhs.eval(context)
        lhs_value = rhs.eval(context)
		if operand == '+':
            return lhs + rhs
        elif operand == '-':
            return lhs - rhs
        ...

# lhs 是 left hand side 的缩写，rhs 同理

当然，在我们实现的表达式语法里，还需要支持向量运算。原理一样，但在求解时需要区分子表达式是数字字面量还是向量。

6. 总结

至此，我们实现了一个非常简单的表达式解析执行器。我们的目的主要是为了实现自定义的 JsonRoute 表达式。相比朴素的 jsonpath，我们加入了计算过程，并且支持向量运算，使用起来非常方便。

ay27的个人小站